Measurement Uncertainty Analysis – Power Reference Level Test
Measurement Introduction
B-4 Agilent E4416A/E4417A Service Guide
:
The equation above includes the worst-case mismatch magnitude 2P
s
P
d
and is in the
form where various powers can be multiplied by the equation to find worst-case
power levels with respect to mismatch.
Note From the above mismatch uncertainty equation if P
d
is zero, for example, the
8478B sensor is exactly 50 ohms then there is NO mismatch uncertainty.
This has not yet been achieved but efforts will be made in the future to try to
achieve as near as possible to a ‘zero’ level of mismatch uncertainty and
hence have negligible mismatch when calibrating products.
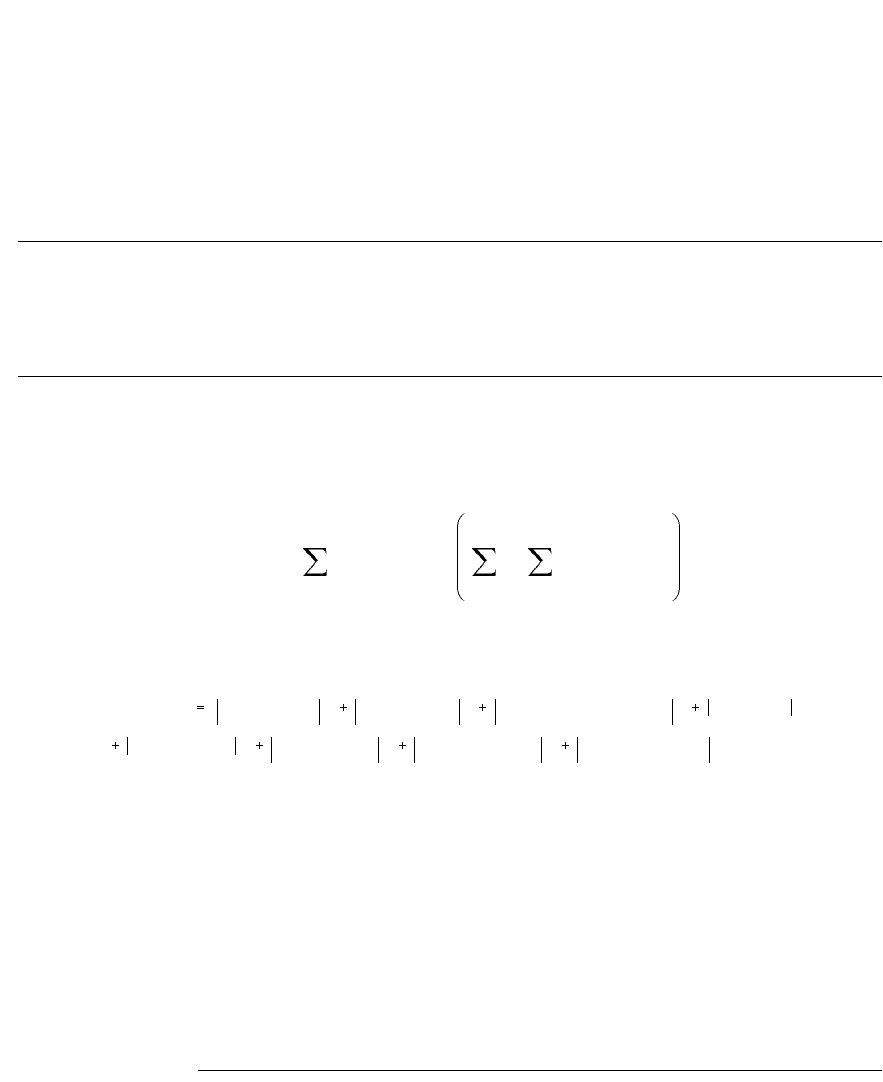
Uncertainty Equation
General form of uncertainty equation is:
Hence,
Assuming that there is no correlation exists between the 8 input variables.
Voltage Measurements Uncertainty
Since the manufacturer’s data is used to determine the standard uncertainty, the
analysis used is the Type A method.
The 3458A DMM Uncertainty is calculated with reference to the Appendix ‘A’ of the
3458A Operating Manual.
M
s
Uncertainty 1 1 2P
s
P
d
±()
⁄
=
u
2
y() c
2
i
u
2
x
i
()
i1=
N
2c
i
c
j
ux
i
x
j
,()
ji1+=
N
i1=
N
+=
u
2
1mW()CV
0
uV
0
()
⋅
2
CV
1
uV
1
()
⋅
2
CV
comp
uV
comp
()
⋅
2
CR u R()
⋅
2
CCF u CF()
⋅
2
CM
s
uM
s
()
⋅
2
C
Rep
u Rep()
⋅
2
C
Drift
u Drift()
⋅
2
